Very Very Large Transformers

Transformers Models: Basics

The transformer architecture of (Vaswani et al, 2017) has been transformative in the sense that is has quickly replaced more classical RNN architectures as the basic block for building large-scale structured prediction model. A TF learns to transform a structured linguistic object (typically a string) into a sequence of numerical representations that can then be used for multiple purposes: machine translation, as in the original paper; language modeling and more generally text generation (summarisation, simplification, etc), and more recently representation learning via the masked language modelling task (Devlin et al, 2019).

In words, a TF learns to turn context-free lexical embedding into contextual representations: each computation layer recombines in a series of 2 main operations all the input representations, to yield the input for the next layer. Given a sentence represented as a list of vectors \(I^l= [h_1^{l-1} \dots h_T^{l-1}]\) at the input of layer \(l\), the most basic operation is the attention operation which will compute a similarity between each input \(h_i^{l-1}\) and all the other inputs in \(I_l\) in a vector \(\alpha^l\) of length \(T\). Once normalized in \(\alpha_i\), these coefficients are used to compute the updated representation \(h_i^{l} = \sum_j \alpha_i^l h_j^{l-1}\), which will be then be added to \(h_i\), normalized, and passed through a feed forward layer before being propagated to the upper layers (details omitted).

Since the first publication, these models have been extensively dissected and analyzed, a very nice starting point beeing the literate reimplementation by S. Rush or the illustrated version by J. Alammar. Open source implementations abound, and trained models for multiple tasks and language can be downloaded from the HugginFace Transformer repos. Many derived models have been proposed extending the capacities of Transformers in several directions giving rise to a full family of models. in the sequel, we focus on attempts at developing larger models, also recently surveyed in (Tay et al, 2020).

Extending the depth

GPT-* denotes a family of models of increasing size and depth introduced over the years by scholars from OpenAi, (which incidentally, is less and less open). The core architecture is a Transformer language model with self-attention, trained with an increasing number of heads and layers. GPT-2 was already so powerful that the large-scale models could not be released to the public (sic!); GTP-3 is a much larger beast (a 100x increase with respect to GPT-2), comprising 175B parameters, and trained with a corpus of more than 400B (BPE) tokens collected from multiple sources that are represented in the Common Crawl corpus where a large part of the effort has been cleaning the corpus.

Typical parameter size of the model are in the cited paper Table 2.1, where we see variations accross the number of heads (from 12 to 96), their size (64 or 128), the number of layers (from 12 to 96), the internal dimension of the vectors (from 768 = 1264 to 12288 = 96128) and the size batch. The length of context is fixed (2048 BPE tokens). Accomodating such numbers also implies a remarkable engineering effort (distribution etc), and small adaptations to the original transformer model to accomodate sparsity in the attention computation. The authors just mention using 'alternating dense and locally banded sparseattention patterns in the layers of the transformer, similar to the Sparse Transformer', plus access to "a high-bandwidth cluster provided by Microsoft" (most likely containing a very large number of GPus V100 cards) - possibly related to MS anouncement of an AI-based computing infrastructure hosting 10000 V100 GPU cards.

GPT-3 and understanding

https://medium.com/@ChrisGPotts/is-it-possible-for-language-models-to-achieve-language-understanding-81df45082ee2

Artificial tests

GPT-3 was also tested with symbolic calculus tasks on numbers (additions, multiplications, etc) and strings (anagrams, read backwards). Only the largest models with zero-shot / few-shot learning does anything good; in particular it solves 2 and 3 digit addition / substraction almost perfectly. Multiplication and string problems seem much more difficult. The issues of GPT-3 with string problems has been analyzed in depth by Melanie Mitchell, who knows some' about string problems. Her conclusions are worth reproducing here: "All in all, GPT-3’s performance is often impressive and surprising, but it is also similar to a lot of what we see in today’s state-of-the-art AI systems: impressive, intelligent-seeming performance interspersed with unhumanlike errors, plus no transparency as to why it performs well or makes certain errors. And it is often hard to tell if the system has actually learned the concept we are trying to teach it."

Multilinguality in GPT-3

For English the number of words: 181 014 683 608 - 181M (meaning BPE would more than double this ?), for French 3 553 061 536 (3.5M) which is only 1.81% still already monstruous - CamemBERT contains 23B, Flaubert only 12B. Another view on this number is that it would correspond to about All these numbers are from the OpenAI's github repos. Numbers for translation are reasonably bad (when fully unsupervised); with few shot supervision it gets much better especially when translating into English.

The exact details of the task are in the appendix. For the zero-shot model, the prompt is "What is the French Translation of "This English Sentence ?". For the few shot models, the training examples were was "This English sentence = Cette phrase française"

Additional sources: * https://medium.com/@bechr7/gpt-3-an-overview-da5d503c9ea8 * https://www.gwern.net/GPT-3#prompts-as-programming

Enlarging the context

Another direction of research has been the extension of the context window. While the initial model only considered a sentencial context, the need to enlarge the context window has quickly emerged, for instance to make the output of a language generating transformer more consistent, or, in machine translation, to model supra sentential phenomena, or more generally discourse related phenomena.

Recall that in a nutshell, the Transformer architecture transforms a structured context (a sequence of tokens, could also be a tree or a graph) into a single numerical vector. The core operation in this transformation is the iterative computation of each individual token's representation based on their similarity to other tokens in the context. In equations, representation \(\tilde{h}_i^{kl}\) for position \(i\) in layer \(l\) is computed by head \(k\) as:

with \(Q^{kl}, K^{kl}, V^{kl}\) parameter matrices associated to these head and layer, \(d\) is the model internal dimension, and \(d_k\) is the head size with value \(d/k\). The output of these \(k\) computations are then concatenated and passed through a feedforward layer with ReLU activation; each of these steps also includes a summation with \(H^{l-1}\) and a layer normalization (see Figure, borrowed from this post).

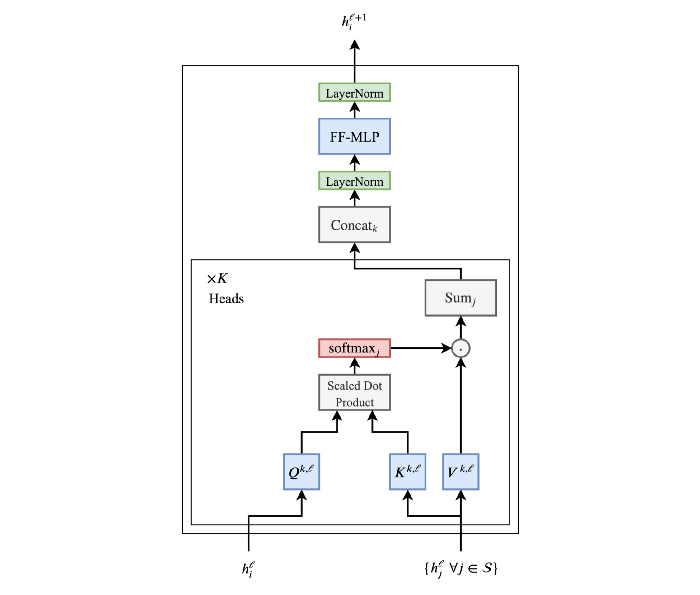
These operations are performed simultaneously for all positions (and for a full batch of them), meaning that the matrix operations actually imply the whole of \(H^l\) instead of just one line or one column. The attention computation has complexity \(O(T^2)\), is performed \(k\) times for each of the \(l\) layers; for gradient computation, it is also needed to store the entire attention matrix of size \((T^2)\). These are the main obstacles towards enlarging the transformer context.

Passing information between contexts

A remarkable benefit of the Transformer architecture is that it makes consecutive contexts independent from each other, enabling to parallelize the computation. (Dai et al, 2019) explain why this can also be viewed as an issue, both computationally (the same computations are repeated multiple times) and from a model perspective (the system has a fixed past horizon). Their proposal, Transformer-XL is to reintroduce some recurrence, and to augment the context representation with hidden states computed at past time frames (note that these values are fixed, and do not propagate any gradients to earlier time frames).

Improving the time complexity

Improving on the time complexity requires to speed up the dot product operations involved in the attention. There are of course generic methods to speed up computation (eg. use half precision float representations), that we do not discuss any further here. One generic method that does not work though, is to use sparse matrix operations, which are hard to accelerate on GPUs. [004.07320]

One specific way to proceed is to reduce the number of neighbours to a fixed size. In (Liu et al, 2018) this is first done by restricting the attention computation to blocks of limited size: this means that the representation of a token only recombines the representation of tokens within the same block. This reduces the contextualization of token representations, but also creates boundary effects at the frontier between block. An alternative (Memory compressed attention) explored in the same work use strided convolutions to reduce the number of neighbors, which preserving the global context.

Boundary effects can also be avoided by considering neighbors in a (sliding) windows of \(S\) words, which means that only the near-diagonal terms of the attention matrix will be computed. If context is localized in the lower layers, it still remains global at the upper layers as the influence of more distant words diffuses in the network. A further trick is to "dilate" these local contexts to speed up the diffusion in the network. To preserve the overall performance, a critical aspect is to make sure that a restricted number of positions still keep a global view over the full input, meaning that they attend to (and are attended to) by all positions. These positions can be described as performing local summaries that are propagated through the entire network. Having one such position every \(\sqrt{T}\) block of length \(\sqrt{T}\) ensures an overall \(O(T\sqrt{T})\) complexity for the attention computation. Such methods are used notably in the Sparse Transformer of (Child et al, 2019), in the Longformer of Beltagy et al (2020), and also employed in the GPT-3 architecture (Brown et al 2020) presented above. Introduced in (Ye et al, 2020), the Binary-Tree Transformer describes an alternative way to combine local and global attention patterns by explicitly organizing the propagation of attention in a (binary) tree structure: each token's representation recombines local neighbors, as well as distant tokens whose representations are first condensed in spans representations organized in a tree, which means that each token only needs to compute attention scores with \(O(\log(T))\) other nodes. In this approach, the root span representation remains the only representation that integrates the full context in its representation. On a related issue, (Rae \& Razavi, 2020) show that global attention is more important in the upper than in the lower levels.

The paper by Zaheer et al, (2020) finally introduces the Long Bird which somehow generalizes these ideas by introducing neighbor graphs specifying, for each position \(i\), the sets of other positions that are used in the computation of \(\tilde{h}^{kl}_i\). In addition to the local context, and to global tokens, the authors propose to also add a random component by adding random neighbors - by choosing specific random graphs, they show that these random neighbors help speed up "diffusion" of information amongst tokens. Moreover, these authors also prove that it is possible to enforce sparsity in the neighbor graph without changing the computational ability of the architecture (which remains Turing complete). Also note that these approaches will imply the definition of supplementary meta-parameters: size of the context window, number (and position) of "global" tokens, size of the random graph, etc.

Note that parsity can also be enforced without setting a parameter, by replacing the costly \(\operatorname{softmax}\) operator by the no-less costly \(\operatorname{sparsemax}\) (Niculae & Blondel, 2017), which however will make sure that \(\alpha^{kl}\) mostly contains \(0\), which could speed up further computations. This approach is described in (Correia et al, 2019), where the focus is however more on the interpretability side than on computational issues. Indeed, learned sparsity patterns make the contribution of each head much easier to interprete.

Another way to speed up this computation is to use approximations: in the Reformer of Kitaev et al, (2019), locally-sensitive hashing is used to identifiy the most significant terms in the summation (corresponding to the most similar neighbours), thereby also yielding sparse attention matrices and computational gains. Another, much simpler way, to save compute time (and space) is to take \(Q^{kl} = K^{lk}\), which seems to have hardly any impact on performance. The Linformer approach of Wang et al (2020) rests on the observation that the computation performed by heads can be approximated by the product of two low ranks matrices. Furthermore, these low rank matrices can be obtained by introducing two random matrices for each head, one to project the \(V^{kl} I^{l-1}\) term (\(T \times{} d_k)\) into a \((S \times{} d_k)\) matrix (through the multiplication by a \(S \times T\) matrix), the other to project \(K^{kl} I^{l-1}\) also into a \((S \times d_k )\) matrix. As a result, the term in the \(\operatorname{softmax}\) outputs a \(T\times S\) matrix (instead of \(T \times t\)). By choosing \(T \gg S\), we get the announced complexity reduction, at almost zero cost in terms of performance. As in other papers, the authors show that parameter sharing (here sharing the projection matrices across layers) can also help speed up the computation without harming performance (too much).

The Performer: http://ai.googleblog.com/2020/10/rethinking-attention-with-performers.html

The "Sinkhorn transformer" Sparse Sinkhorn attention

The Linear Transformer

The Fastformer [https://arxiv.org/abs/2108.09084]

[Improving the space complexity]

Use revertible gradients - (Kitaev et al)

use gradient checkpointing (Chen et al., 2016) saves memoryby only caching activations of a subset of layers. This does save space, at the cost of an increased training time.